ツイートに対するネットの反応
KUMONグループが社内で規定する、こういう知育玩具の出荷許容公差はどんな感じなのか、凄く知りたい。材質にもよるが、極粗級よりも更に粗い社内基準を規定している可能性もある。
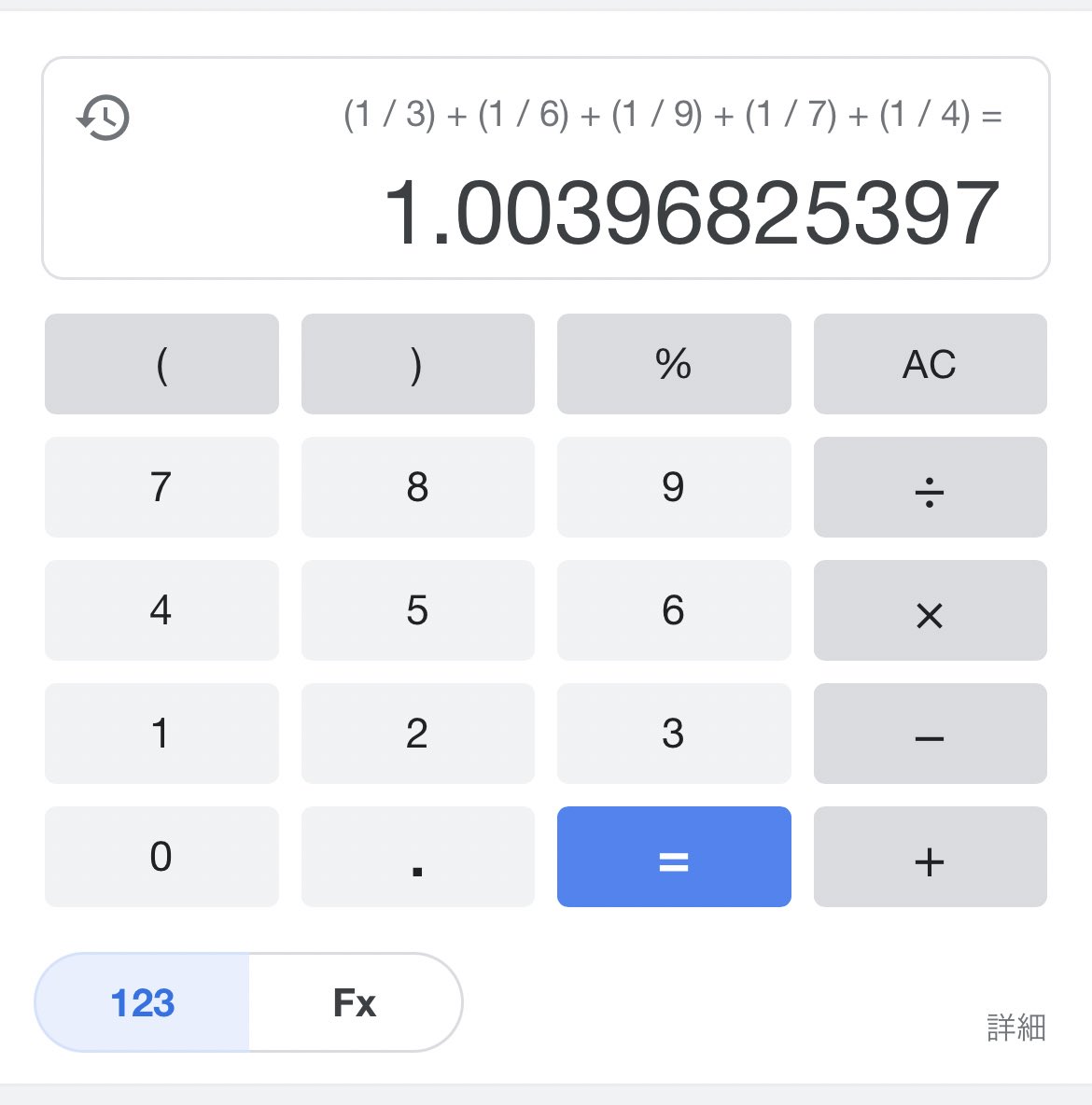
最初3、7、4、9、6の最小公倍数を一生懸命考えていたけど、頭がフットーしそうになったので大人しく電卓に頼ることにした。
うん。合わないwww
0.004だけ合わないww https://t.co/8fl6XYwTPN

midnightwalker@深夜休止中@mghinditweklar
ピースと枠の間にどうしてもガタがあるもんで、本来収まらないはずの組み合わせでも差が吸収されて入っちゃうのよね(´・ω・`) @yugokitajima
計算前:1/7が混じっている時点でおかしいだろwww
計算後:(あ…)
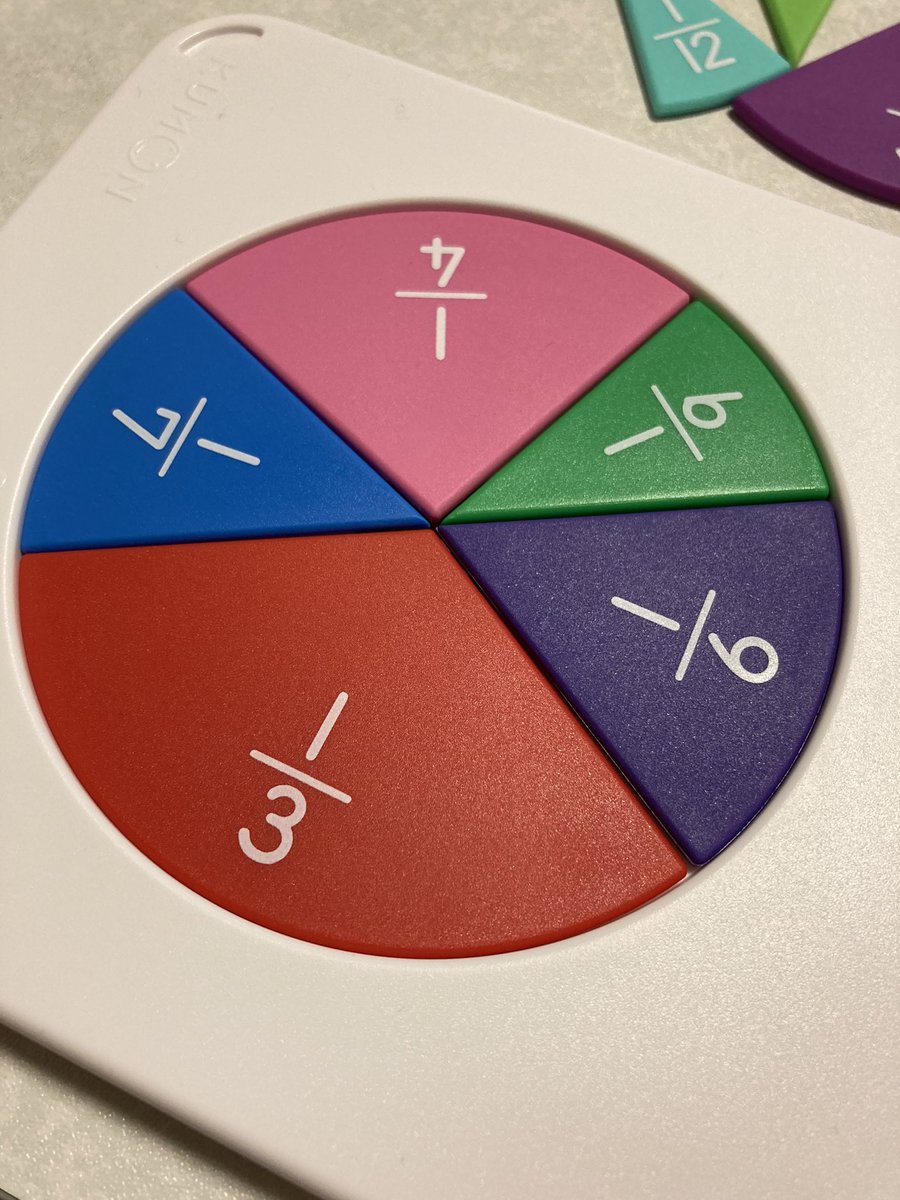
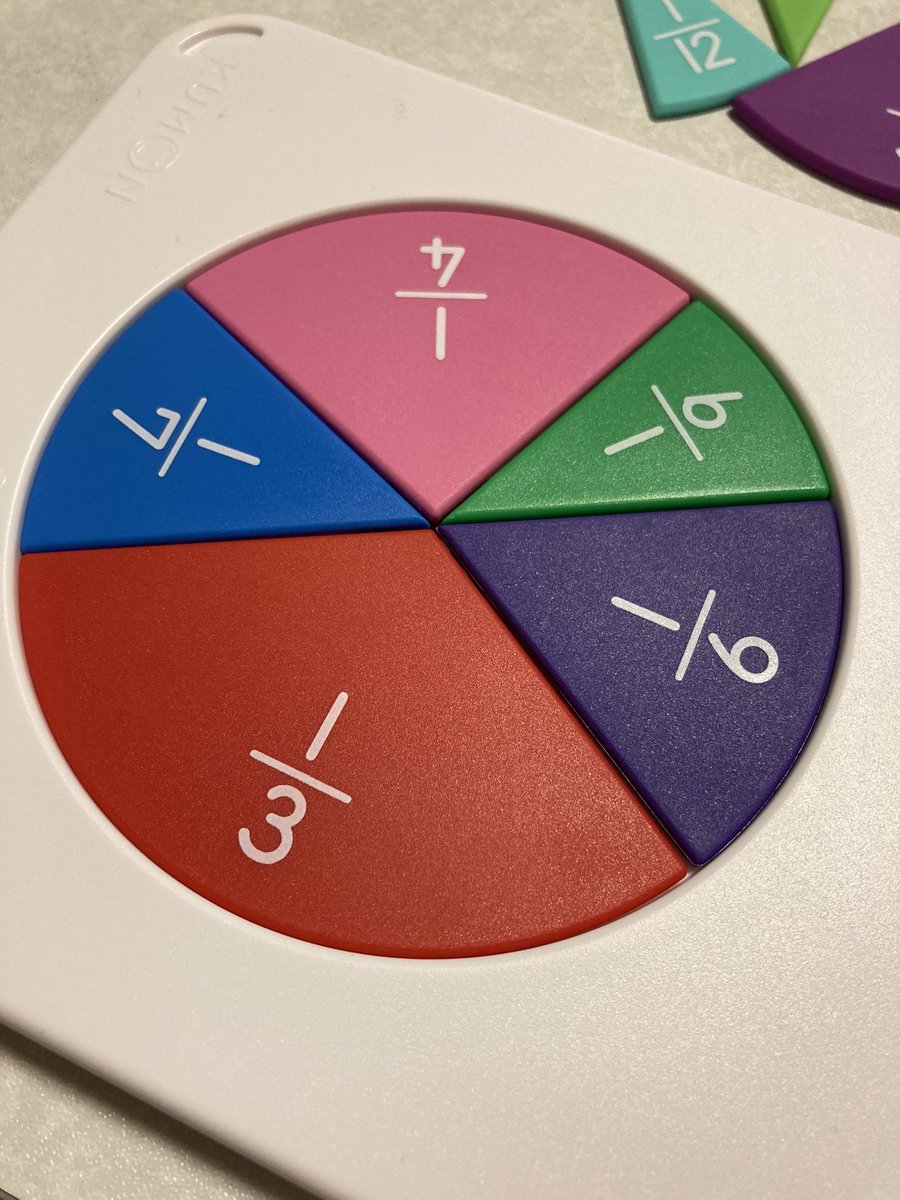
1/3+1/4+1/6+1/7+1/9=253/252=1.003968…
面白い…ただ、Amazonのレビューによるとトレーに対してピースが小さ目らしく、少々合わなくてもハマってしまうらしい。仮に円の直径10cmとすると253/252は1.2mm超過だが、レビューによるとその倍の誤差121/120でもハマるらしい。
これ家族がサンタさんにもらって、やだってなってうちにくれたやつや。
うちもらったのかけ算のなんかやったわ。
その時のサンタさん勉強押してた。
数字のチョイスが良いね。
暗算でもおかしいということが導きやすい
1 – (1/3 + 1/6 + 1/4) = 1/4
残る 1/7 + 1/9 ≠ 1/4 なので、この図はおかしい。
1 < 1/3 + 1/4 + 1/6 + 1/7 + 1/9 でハマっちゃうのはアカン気もするけど
あーもしや「測定の精度」の逆の問題かな。
「物理の計算精度は向上はしても現実とイコールに必ずしもならない」という有効数字の話が画像の本の解説だけど、引用RTはその逆で、数学の表現を基に現実の工作をすると、その際もまた誤差は付きもので人の目には同じに見えるものができるということかな? https://t.co/g9VWRg6Vyc



これリプみてたらみんな全部足してるけど1/6と1/3で半分で1/4もあるんなら残りの1/4≠1/9+1/7=16/63て簡単に計算できそうなんだよな